Cubical marching squares is an isosurface extraction algorithm based on the marching cubes algorithm. This post is about my journey implementing it. I also made a video about it. My implementation is available on github.
Why?
For some reason I got interested in isosurface extraction algorithms. The first one I implemented was the Marching Cubes (MC) algorithm. Next I explored the Dual Contouring (DC) algorithm. And now I wanted to try the Cubical Marching Squares (CMS) algorithm. Visualizing these algorithms has become a hobby of mine.
While DC or MC are widely used, they aren’t always optimal. The main limitation of MC is that it assumes a smooth surface and doesn’t preserve sharp features. Also producing adaptive- or multi-resolution meshes requires additional patching, such as the Transvoxel algorithm. DC can preserve sharp features, but it can produce non-manifold meshes. CMS can produce manifold meshes, preserve sharp features and produces multi-resolution meshes out of the box.
The algorithm
The core idea behind the CMS algorithm is to unfold the cube into 6 faces, and then use the Marching Squares algorithm on each face. If you keep track of which edges are shared between faces, you can fold the cube back together and get a consistent mesh. If you process each face in the lattice once (every face is shared by two cells) this guarantees that the entire cell is always consistent, unlike MC where ambiguities can occur.
Marching Squares is a 2D algorithm, the extracted isosurface/isoline is a line; in 3D isosurface is a surface. CMS algorithm forms loops from these line segments generated by Marching Squares, and then triangulates the loops as triangle fans.
The algorithm preserves sharp features by allowing placing new vertices either on the faces (during the Marching Squares step) or inside the 3D cell (calculating a new apex point for the triangle fan). The sharp vertices are found by using the Hermite data. In 2D it comes down to finding the intersection of two tangent lines. In 3D it’s more complicated because of possible rank deficiencies, but the idea is similar.
Additionally CMS deals with face and internal ambiguities.
Marching squares has two ambiguous cases, and CMS resolves these by avoiding self-intersections.
Similarly in 3D, the diagonal ambiguity can be resolved by avoiding self-intersections. The alternative triangulation connects two segment loops into a ’tunnel’, which solves the self-intersection problem.
However, I didn’t see how their method for internal ambiguities could work for anything other than the 8 diagonal cases (case 4 and maybe 13, see below).
If self-intersection occurs in any of the other cases with multiple triangle fans, then the triangulation seems way more complicated and as far as I could tell isn’t covered (cases 6, 7 etc).
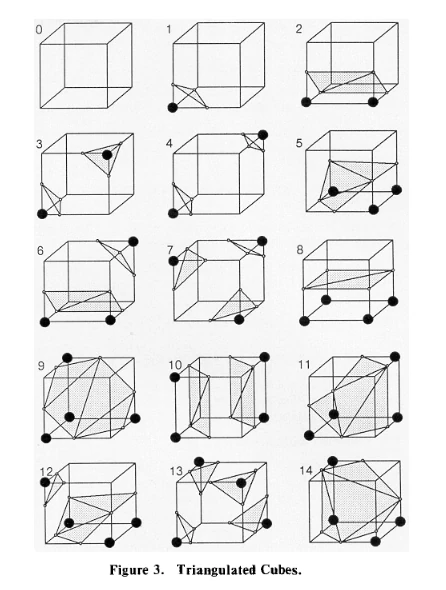
MC cases (from the MC paper)
The CMS paper also proposes using an octree instead of an uniform grid, but the algorithm works fine on uniform grids as well. I think that’s all of the major differences to MC, the rest is just software engineering.
My video about the algorithm:
My implementation
Implementation.
It’s in C#, but as of writing this post there’s also a branch with C++ code, might merge it later.

Example results
Generally, it seems to perform as expected, but there are a lot of edge cases to deal with and the paper doesn’t go into much detail about them.
In the picture below I’ve highlighted some defects in blue. The dark line around the square prism is drawn to make the shape more clear because there is no shading.
The bottom right one on the prism is due to the 2D sharp feature generation not being aware of the base plane of the prism, not sure if this can be fixed. I think the other ones happen when during 3D sharp feature extraction there’s more than 2 planes, but the correct feature is a specific edge. The algorithm finds the tip of the prism, but you really want to place the vertex on the edge that’s within the cell. I discard sharp vertices that are out of cell, so it uses the average position as triangle fan central vertex by default, creating this ‘dent’ defect. Increasing the hermite data resolution usually fixes almost all defects.
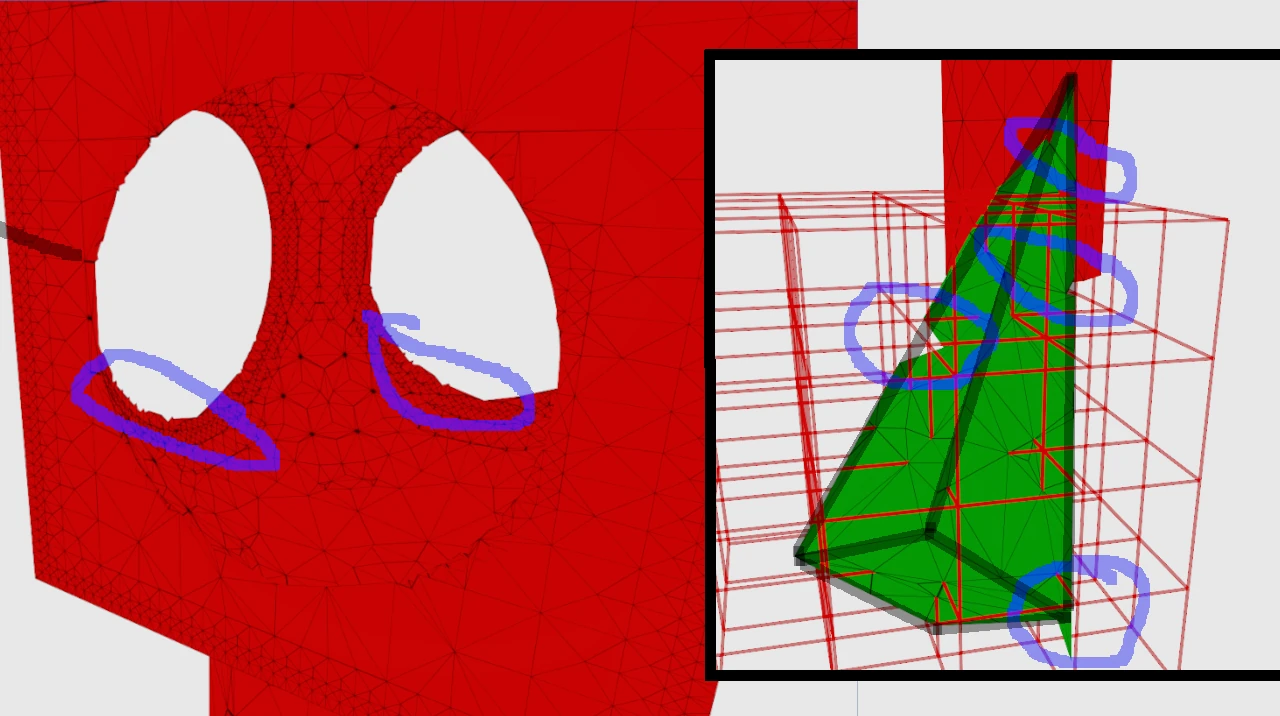
Mesh defects
It was very tedious to track all the edges and faces during octree cell subdivision, other than that it wasn’t too difficult to implement. It still took weeks to get it to reasonable enough state. The most complicated part was handling internal ambiguities, which required using Dynamic Programming. Not sure if I got it right, but my code seemed to work on the few test cases I tried.
Conclusion and future work
Overall, I think it’s a good algorithm. Ideally I would like to modify it so that you could render terrains with LOD, but that seems like a lot of work and I’m not sure if I have any use for it. The algorithm assumes that the underlying hermite data is fixed resolution, so you’d have to modify it to work with continuous LOD. In my implementation I also heavily assume that the octree doesn’t change. It might be better to take the more traditional approach of patching chunks of uniform resolution. Might just move on to something else though.